To what volume will the cylinder expand to if it must expand against a pressure of 817.77 mmHg.

Learning Objectives

By the end of this section, you will exist able to:

• Place the mathematical relationships between the various properties of gases
• Utilise the platonic gas law, and related gas laws, to compute the values of various gas properties nether specified conditions

During the seventeenth and especially eighteenth centuries, driven both by a desire to understand nature and a quest to make balloons in which they could wing (Figure one), a number of scientists established the relationships between the macroscopic physical properties of gases, that is, pressure, book, temperature, and amount of gas. Although their measurements were not precise past today'due south standards, they were able to decide the mathematical relationships between pairs of these variables (due east.g., pressure and temperature, force per unit area and volume) that hold for an platonic gas—a hypothetical construct that real gases guess under sure conditions. Somewhen, these private laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite authentic for low pressures and moderate temperatures. Nosotros will consider the key developments in private relationships (for pedagogical reasons not quite in historical order), and so put them together in the platonic gas police.

Figure 1. In 1783, the starting time (a) hydrogen-filled balloon flying, (b) manned hot air balloon flying, and (c) manned hydrogen-filled balloon flying occurred. When the hydrogen-filled balloon depicted in (a) landed, the frightened villagers of Gonesse reportedly destroyed information technology with pitchforks and knives. The launch of the latter was reportedly viewed by 400,000 people in Paris.

Pressure and Temperature: Amontons'due south Law

Imagine filling a rigid container fastened to a pressure level gauge with gas and so sealing the container so that no gas may escape. If the container is cooled, the gas within likewise gets colder and its force per unit area is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If nosotros heat the sphere, the gas inside gets hotter (Figure 2) and the pressure increases.

Figure 2. The effect of temperature on gas pressure: When the hot plate is off, the pressure of the gas in the sphere is relatively low. As the gas is heated, the force per unit area of the gas in the sphere increases.

This relationship between temperature and pressure is observed for any sample of gas bars to a abiding volume. An case of experimental pressure level-temperature data is shown for a sample of air under these atmospheric condition in Effigy three. We find that temperature and force per unit area are linearly related, and if the temperature is on the kelvin scale, so P and T are directly proportional (over again, when volume and moles of gas are held abiding); if the temperature on the kelvin scale increases by a certain cistron, the gas pressure increases by the same factor.

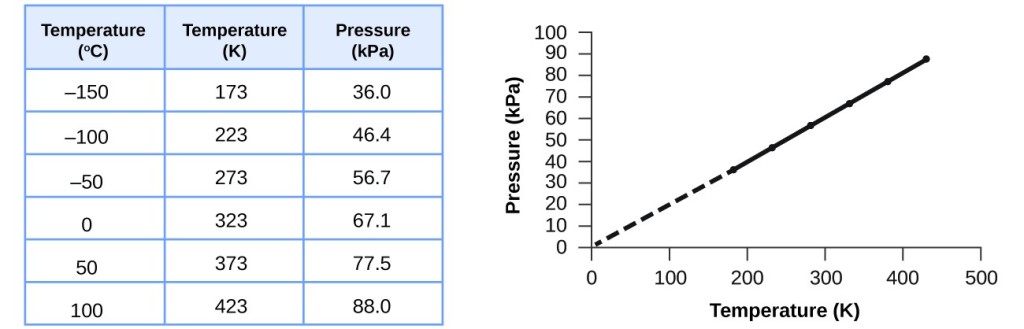
Effigy iii. For a constant volume and amount of air, the force per unit area and temperature are directly proportional, provided the temperature is in kelvin. (Measurements cannot be made at lower temperatures because of the condensation of the gas.) When this line is extrapolated to lower pressures, it reaches a pressure of 0 at –273 °C, which is 0 on the kelvin scale and the everyman possible temperature, called absolute zero.

Guillaume Amontons was the first to empirically establish the relationship betwixt the pressure and the temperature of a gas (~1700), and Joseph Louis Gay-Lussac determined the relationship more precisely (~1800). Considering of this, the P–T relationship for gases is known as either Amontons'south law or Gay-Lussac's police. Under either name, it states that the pressure of a given amount of gas is direct proportional to its temperature on the kelvin scale when the book is held constant. Mathematically, this can be written:

[latex]P\propto T[/latex]

[latex]P=\text{abiding}\times T[/latex]

[latex]P=thou\times T[/latex]

where ∝ means "is proportional to," and thousand is a proportionality constant that depends on the identity, amount, and book of the gas.

For a confined, abiding volume of gas, the ratio [latex]\frac{P}{T}[/latex] is therefore constant (i.e., [latex]\frac{P}{T}=m[/latex] ). If the gas is initially in "Condition 1" (with P = P ₁ and T = T _ane), and so changes to "Status 2" (with P = P ₂ and T = T ₂), we have that [latex]\frac{{P}_{i}}{{T}_{i}}=k[/latex] and [latex]\frac{{P}_{two}}{{T}_{2}}=g,[/latex] which reduces to:

[latex]\frac{{P}_{1}}{{T}_{one}}=\frac{{P}_{2}}{{T}_{ii}}[/latex]

This equation is useful for pressure level-temperature calculations for a bars gas at abiding volume. Note that temperatures must be on the kelvin calibration for any gas police calculations (0 on the kelvin scale and the everyman possible temperature is called absolute null). (Also note that there are at least iii ways nosotros tin can describe how the pressure of a gas changes as its temperature changes: We can use a table of values, a graph, or a mathematical equation.)

Example ane: Predicting Change in Pressure with Temperature

A can of pilus spray is used until it is empty except for the propellant, isobutane gas.

1. On the can is the warning "Shop only at temperatures beneath 120 °F (48.viii °C). Do not incinerate." Why?
2. The gas in the tin can is initially at 24 °C and 360 kPa, and the can has a volume of 350 mL. If the can is left in a car that reaches 50 °C on a hot day, what is the new pressure in the tin can?

Check Your Learning

A sample of nitrogen, N₂, occupies 45.0 mL at 27 °C and 600 torr. What pressure will it have if cooled to –73 °C while the volume remains constant?

Volume and Temperature: Charles's Law

If we make full a airship with air and seal information technology, the balloon contains a specific amount of air at atmospheric pressure, permit'due south say ane atm. If nosotros put the balloon in a refrigerator, the gas inside gets cold and the airship shrinks (although both the amount of gas and its pressure remain constant). If we brand the balloon very common cold, it will shrink a great deal, and it expands again when it warms upwardly.

This video shows how cooling and heating a gas causes its volume to decrease or increase, respectively.

These examples of the effect of temperature on the volume of a given amount of a bars gas at constant pressure are true in full general: The volume increases equally the temperature increases, and decreases equally the temperature decreases. Volume-temperature data for a ane-mole sample of methane gas at 1 atm are listed and graphed in Figure four.

Figure 4. The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure level of ane atm. If the temperature is in kelvin, volume and temperature are direct proportional. The line stops at 111 Yard considering methane liquefies at this temperature; when extrapolated, information technology intersects the graph'southward origin, representing a temperature of accented nada.

The relationship between the volume and temperature of a given corporeality of gas at constant pressure is known as Charles'due south police in recognition of the French scientist and balloon flying pioneer Jacques Alexandre César Charles. Charles'due south police force states that the volume of a given amount of gas is straight proportional to its temperature on the kelvin calibration when the pressure is held constant.

Mathematically, this tin can be written as:

[latex]V\propto T[/latex]

[latex]5=\text{constant}\cdot T[/latex]

[latex]V=k\cdot T[/latex]

with k beingness a proportionality constant that depends on the corporeality and force per unit area of the gas.

For a confined, abiding pressure level gas sample, [latex]\frac{5}{T}[/latex] is constant (i.eastward., the ratio = yard), and as seen with the V–T relationship, this leads to another class of Charles's police force:

[latex]\frac{{V}_{1}}{{T}_{i}}=\frac{{Five}_{2}}{{T}_{2}}[/latex]

Instance 2: Predicting Change in Book with Temperature

A sample of carbon dioxide, CO₂, occupies 0.300 L at 10 °C and 750 torr. What volume will the gas have at 30 °C and 750 torr?

Check Your Learning

A sample of oxygen, O₂, occupies 32.2 mL at 30 °C and 452 torr. What book will it occupy at –70 °C and the same pressure level?

Example 3: Measuring Temperature with a Volume Change

Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a item hydrogen gas thermometer has a volume of 150.0 cmⁱⁱⁱ when immersed in a mixture of water ice and water (0.00 °C). When immersed in boiling liquid ammonia, the book of the hydrogen, at the same pressure, is 131.7 cm^three. Notice the temperature of boiling ammonia on the kelvin and Celsius scales.

Check Your Learning

What is the volume of a sample of ethane at 467 G and 1.1 atm if it occupies 405 mL at 298 K and i.1 atm?

Volume and Pressure: Boyle's Law

If we partially fill up an closed syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C. If we slowly push in the plunger while keeping temperature constant, the gas in the syringe is compressed into a smaller volume and its pressure increases; if we pull out the plunger, the volume increases and the pressure decreases. This example of the issue of volume on the pressure of a given amount of a confined gas is true in general. Decreasing the volume of a contained gas volition increment its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases past a certain factor, the force per unit area decreases by the same factor, and vice versa. Volume-pressure data for an air sample at room temperature are graphed in Figure 5.

Figure 5. When a gas occupies a smaller volume, it exerts a higher pressure level; when it occupies a larger volume, it exerts a lower force per unit area (assuming the amount of gas and the temperature practise not change). Since P and Five are inversely proportional, a graph of one/P vs. V is linear.

Different the P–T and V–T relationships, force per unit area and volume are not straight proportional to each other. Instead, P and Five exhibit changed proportionality: Increasing the pressure level results in a decrease of the book of the gas. Mathematically this can be written:

[latex]P\propto one\text{/}V\text{ or }P=thousand\cdot 1\text{/}V\text{ or }P\cdot V=chiliad\text{ or }{P}_{ane}{5}_{i}={P}_{2}{V}_{two}[/latex]

Figure six. The relationship between pressure level and volume is inversely proportional. (a) The graph of P vs. V is a parabola, whereas (b) the graph of (one/P) vs. 5 is linear.

with grand being a constant. Graphically, this human relationship is shown by the straight line that results when plotting the inverse of the pressure [latex]\left(\frac{1}{P}\right)[/latex] versus the volume (V), or the changed of volume [latex]\left(\frac{one}{V}\right)[/latex] versus the pressure (V). Graphs with curved lines are difficult to read accurately at depression or high values of the variables, and they are more difficult to use in plumbing fixtures theoretical equations and parameters to experimental information. For those reasons, scientists oft try to find a way to "linearize" their data. If nosotros plot P versus 5, we obtain a hyperbola (come across Figure vi).

The relationship betwixt the volume and pressure level of a given amount of gas at abiding temperature was beginning published by the English natural philosopher Robert Boyle over 300 years ago. Information technology is summarized in the statement now known as Boyle's law: The volume of a given amount of gas held at constant temperature is inversely proportional to the force per unit area under which information technology is measured.

Example 4: Volume of a Gas Sample

The sample of gas in Figure 5 has a volume of 15.0 mL at a pressure of 13.0 psi. Make up one's mind the pressure of the gas at a volume of 7.v mL, using:

1. the P–V graph in Figure v
2. the [latex]\frac{1}{P}[/latex] vs. V graph in Effigy 5
3. the Boyle's law equation

Comment on the likely accuracy of each method.

Check Your Learning

The sample of gas in Figure 5 has a volume of xxx.0 mL at a pressure of 6.five psi. Determine the book of the gas at a pressure of xi.0 mL, using:

1. the P–V graph in Figure 5
2. the [latex]\frac{1}{P}[/latex] vs. 5 graph in Effigy 5
3. the Boyle's law equation

Annotate on the probable accuracy of each method.

Chemical science in Action: Breathing and Boyle's Law

What exercise you do about xx times per minute for your whole life, without interruption, and often without fifty-fifty being aware of it? The answer, of course, is respiration, or breathing. How does it work? It turns out that the gas laws apply here. Your lungs take in gas that your body needs (oxygen) and become rid of waste gas (carbon dioxide). Lungs are fabricated of spongy, stretchy tissue that expands and contracts while you exhale. When you inhale, your diaphragm and intercostal muscles (the muscles betwixt your ribs) contract, expanding your breast cavity and making your lung book larger. The increase in volume leads to a decrease in pressure level (Boyle's law). This causes air to menses into the lungs (from high pressure to depression pressure level). When you breathe, the process reverses: Your diaphragm and rib muscles relax, your chest cavity contracts, and your lung volume decreases, causing the pressure to increase (Boyle's police over again), and air flows out of the lungs (from high pressure to depression pressure). You then breathe in and out again, and again, repeating this Boyle's law wheel for the residue of your life (Figure 7).

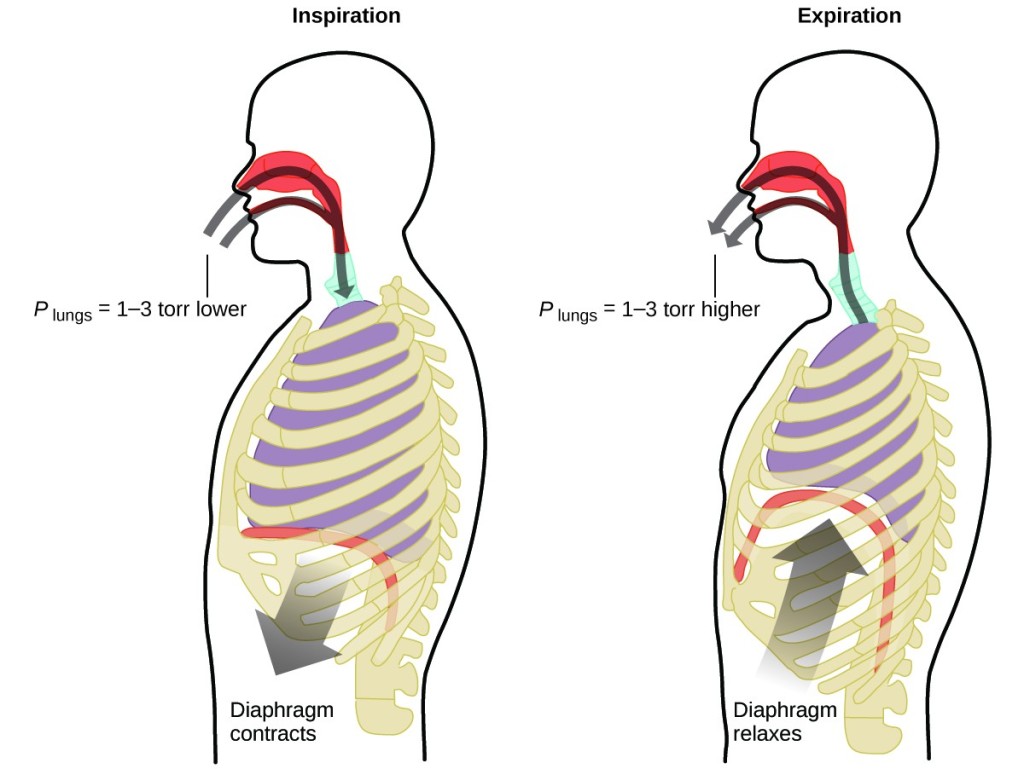
Figure 7. Breathing occurs because expanding and contracting lung volume creates pocket-size pressure differences between your lungs and your environs, causing air to exist drawn into and forced out of your lungs.

Moles of Gas and Volume: Avogadro's Police

The Italian scientist Amedeo Avogadro advanced a hypothesis in 1811 to account for the behavior of gases, stating that equal volumes of all gases, measured under the same weather condition of temperature and pressure, incorporate the same number of molecules. Over time, this relationship was supported by many experimental observations every bit expressed by Avogadro'southward law: For a confined gas, the book (V) and number of moles (n) are directly proportional if the pressure and temperature both remain constant.

In equation grade, this is written as:

[latex]\begin{assortment}{ccccc}5\propto n& \text{or}& V=chiliad\times n& \text{or}& \frac{{V}_{1}}{{n}_{1}}=\frac{{Five}_{2}}{{n}_{2}}\cease{array}[/latex]

Mathematical relationships can as well be determined for the other variable pairs, such as P versus northward, and north versus T.

Visit this interactive PhET simulation link to investigate the relationships betwixt pressure, volume, temperature. and amount of gas. Use the simulation to examine the result of irresolute one parameter on another while property the other parameters constant (as described in the preceding sections on the various gas laws).

The Ideal Gas Law

To this point, four separate laws take been discussed that chronicle pressure level, volume, temperature, and the number of moles of the gas:

• Boyle's law: PV = constant at constant T and due north
• Amontons's police force: [latex]\frac{P}{T}[/latex] = constant at constant V and n
• Charles'south constabulary: [latex]\frac{5}{T}[/latex] = abiding at constant P and due north
• Avogadro's police: [latex]\frac{5}{northward}[/latex] = constant at abiding P and T

Combining these four laws yields the ideal gas constabulary, a relation between the force per unit area, volume, temperature, and number of moles of a gas:

[latex]PV=nRT[/latex]

where P is the pressure of a gas, V is its volume, n is the number of moles of the gas, T is its temperature on the kelvin scale, and R is a constant called the ideal gas constant or the universal gas abiding. The units used to express pressure, volume, and temperature will determine the proper form of the gas constant equally required by dimensional analysis, the nearly ordinarily encountered values being 0.08206 Fifty atm mol^–1 G^–ane and 8.314 J L mol^–1 Yard^–1.

Gases whose backdrop of P, Five, and T are accurately described by the platonic gas law (or the other gas laws) are said to exhibit ideal behavior or to guess the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as volition exist described in a subsequently module of this chapter. Although all the calculations presented in this module presume ideal behavior, this supposition is only reasonable for gases under conditions of relatively low pressure and high temperature. In the last module of this chapter, a modified gas law will be introduced that accounts for the non-ideal beliefs observed for many gases at relatively high pressures and low temperatures.

The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any 4 of these terms will permit use of the ideal gas police force to calculate the fifth term every bit demonstrated in the following example exercises.

Instance 5: Using the Ideal Gas Police force

Methyl hydride, CH₄, is being considered for use as an alternative automotive fuel to replace gasoline. Ane gallon of gasoline could be replaced past 655 g of CH₄. What is the volume of this much methane at 25 °C and 745 torr?

Check Your Learning

Calculate the pressure in bar of 2520 moles of hydrogen gas stored at 27 °C in the 180-50 storage tank of a modern hydrogen-powered car.

If the number of moles of an platonic gas are kept abiding under two different sets of conditions, a useful mathematical relationship called the combined gas law is obtained: [latex]\frac{{P}_{1}{V}_{1}}{{T}_{i}}=\frac{{P}_{2}{V}_{ii}}{{T}_{2}}[/latex] using units of atm, L, and K. Both sets of conditions are equal to the product of n × R (where n = the number of moles of the gas and R is the platonic gas police constant).

Instance 6: Using the Combined Gas Constabulary

Figure 8. Scuba divers utilise compressed air to breathe while underwater. (credit: modification of piece of work by Mark Goodchild)

When filled with air, a typical scuba tank with a volume of xiii.2 L has a pressure of 153 atm (Effigy 8). If the h2o temperature is 27 °C, how many liters of air volition such a tank provide to a diver'due south lungs at a depth of approximately seventy feet in the ocean where the pressure is three.13 atm?

Check Your Learning

A sample of ammonia is found to occupy 0.250 L under laboratory atmospheric condition of 27 °C and 0.850 atm. Find the book of this sample at 0 °C and 1.00 atm.

The Interdependence between Sea Depth and Pressure in Scuba Diving

Figure 9. Scuba divers, whether at the Great Barrier Reef or in the Caribbean, must be aware of buoyancy, pressure equalization, and the corporeality of time they spend underwater, to avoid the risks associated with pressurized gases in the body. (credit: Kyle Taylor)

Whether scuba diving at the Great Barrier Reef in Australia (shown in Figure ix) or in the Caribbean, defined must understand how pressure affects a number of problems related to their comfort and safety.

Pressure level increases with ocean depth, and the force per unit area changes most rapidly as divers achieve the surface. The pressure a diver experiences is the sum of all pressures in a higher place the diver (from the water and the air). Near pressure measurements are given in units of atmospheres, expressed every bit "atmospheres absolute" or ATA in the diving community: Every 33 feet of salt water represents 1 ATA of pressure in addition to 1 ATA of pressure from the temper at bounding main level.

As a diver descends, the increase in pressure causes the body's air pockets in the ears and lungs to shrink; on the ascent, the decrease in pressure causes these air pockets to expand, potentially rupturing eardrums or bursting the lungs. Divers must therefore undergo equalization by adding air to body airspaces on the descent by breathing normally and adding air to the mask by animate out of the olfactory organ or adding air to the ears and sinuses by equalization techniques; the corollary is likewise true on ascent, divers must release air from the body to maintain equalization.

Buoyancy, or the ability to command whether a diver sinks or floats, is controlled by the buoyancy compensator (BCD). If a diver is ascending, the air in his BCD expands because of lower force per unit area according to Boyle'southward police (decreasing the pressure of gases increases the volume). The expanding air increases the buoyancy of the diver, and she or he begins to ascend. The diver must vent air from the BCD or risk an uncontrolled rising that could rupture the lungs. In descending, the increased pressure causes the air in the BCD to compress and the diver sinks much more chop-chop; the diver must add air to the BCD or risk an uncontrolled descent, facing much college pressures well-nigh the ocean floor.

The pressure also impacts how long a diver can stay underwater earlier ascending. The deeper a diver dives, the more compressed the air that is breathed because of increased pressure: If a diver dives 33 anxiety, the pressure is two ATA and the air would be compressed to half of its original volume. The diver uses up bachelor air twice as fast equally at the surface.

Standard Conditions of Temperature and Pressure

We have seen that the book of a given quantity of gas and the number of molecules (moles) in a given volume of gas vary with changes in pressure and temperature. Chemists sometimes make comparisons against a standard temperature and pressure (STP) for reporting properties of gases: 273.15 Grand and 1 atm (101.325 kPa). At STP, an platonic gas has a volume of virtually 22.four L—this is referred to equally the standard molar volume (Effigy ten).

Figure 10. Since the number of moles in a given volume of gas varies with pressure and temperature changes, chemists use standard temperature and pressure (273.xv K and one atm or 101.325 kPa) to report properties of gases.

Cardinal Concepts and Summary

The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure level of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does non modify (Amontons's police). The volume of a given amount of gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law). The volume of a given amount of gas is inversely proportional to its pressure level when temperature is held constant (Boyle's police force). Nether the same weather of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law).

The equations describing these laws are special cases of the ideal gas law, PV = nRT, where P is the pressure level of the gas, V is its book, n is the number of moles of the gas, T is its kelvin temperature, and R is the ideal (universal) gas abiding.

Primal Equations

• PV = nRT

Exercises

1. Sometimes leaving a bicycle in the sunday on a hot twenty-four hours will crusade a blowout. Why?
2. Explicate how the volume of the bubbles exhausted past a scuba diver (Effigy viii) change as they rise to the surface, assuming that they remain intact.
3. I style to state Boyle's law is "All other things being equal, the pressure of a gas is inversely proportional to its book."
   1. What is the meaning of the term "inversely proportional?"
   2. What are the "other things" that must be equal?
4. An alternating mode to state Avogadro's law is "All other things being equal, the number of molecules in a gas is directly proportional to the book of the gas."
   1. What is the meaning of the term "directly proportional?"
   2. What are the "other things" that must be equal?
5. How would the graph in Figure iv change if the number of moles of gas in the sample used to make up one's mind the bend were doubled?
6. How would the graph in Figure 5 change if the number of moles of gas in the sample used to determine the curve were doubled?
7. In addition to the data found in Figure 5, what other information practise we need to observe the mass of the sample of air used to determine the graph?
8. Determine the volume of 1 mol of CH₄ gas at 150 K and 1 atm, using Figure 4.
9. Determine the pressure level of the gas in the syringe shown in Effigy 5 when its volume is 12.5 mL, using:
   1. the appropriate graph
   2. Boyle's police
10. A spray tin is used until information technology is empty except for the propellant gas, which has a pressure of 1344 torr at 23 °C. If the tin is thrown into a fire (T = 475 °C), what will be the pressure in the hot can?
11. What is the temperature of an eleven.2 L sample of carbon monoxide, CO, at 744 torr if it occupies 13.iii Fifty at 55 °C and 744 torr?
12. A 2.50 50 book of hydrogen measured at –196 °C is warmed to 100 °C. Calculate the volume of the gas at the higher temperature, assuming no change in pressure.
13. A airship inflated with three breaths of air has a book of 1.7 50. At the same temperature and pressure, what is the volume of the airship if five more same-sized breaths are added to the balloon?
14. A weather balloon contains 8.80 moles of helium at a pressure of 0.992 atm and a temperature of 25 °C at ground level. What is the volume of the balloon under these conditions?
15. The volume of an automobile air handbag was 66.8 Fifty when inflated at 25 °C with 77.8 1000 of nitrogen gas. What was the pressure level in the bag in kPa?
16. How many moles of gaseous boron trifluoride, BF₃, are independent in a iv.3410 50 bulb at 788.0 Thou if the pressure is one.220 atm? How many grams of BF_three?
17. Iodine, I₂, is a solid at room temperature but sublimes (converts from a solid into a gas) when warmed. What is the temperature in a 73.three mL bulb that contains 0.292 grand of I₂ vapor at a pressure of 0.462 atm?
18. How many grams of gas are present in each of the post-obit cases?
    1. 0.100 Fifty of CO₂ at 307 torr and 26 °C
    2. 8.75 L of C₂H_four, at 378.3 kPa and 483 K
    3. 221 mL of Ar at 0.23 torr and –54 °C
19. A high altitude balloon is filled with i.41 × ten^four L of hydrogen at a temperature of 21 °C and a pressure level of 745 torr. What is the volume of the balloon at a tiptop of 20 km, where the temperature is –48 °C and the pressure is 63.1 torr?
20. A cylinder of medical oxygen has a volume of 35.4 L, and contains O₂ at a pressure of 151 atm and a temperature of 25 °C. What volume of O_ii does this correspond to at normal body conditions, that is, 1 atm and 37 °C?
21. A large scuba tank (Figure 8) with a volume of eighteen L is rated for a pressure of 220 bar. The tank is filled at xx °C and contains enough air to supply 1860 L of air to a diver at a pressure of 2.37 atm (a depth of 45 feet). Was the tank filled to capacity at 20 °C?
22. A 20.0 L cylinder containing 11.34 kg of butane, C₄H₁₀, was opened to the temper. Calculate the mass of the gas remaining in the cylinder if information technology were opened and the gas escaped until the pressure in the cylinder was equal to the atmospheric pressure, 0.983 atm, and a temperature of 27 °C.
23. While resting, the boilerplate 70 kg human male person consumes 14 50 of pure O₂ per hour at 25 °C and 100 kPa. How many moles of O₂ are consumed by a seventy kg man while resting for 1.0 h?
24. For a given amount of gas showing ideal behavior, draw labeled graphs of:
    1. the variation of P with Five
    2. the variation of V with T
    3. the variation of P with T
    4. the variation of [latex]\frac{i}{P}[/latex] with Five
25. A liter of methyl hydride gas, CH_four, at STP contains more than atoms of hydrogen than does a liter of pure hydrogen gas, H₂, at STP. Using Avogadro's police force equally a starting point, explain why.
26. The effect of chlorofluorocarbons (such every bit CCl_twoF₂) on the depletion of the ozone layer is well known. The employ of substitutes, such as CH₃CH_iiF(g), for the chlorofluorocarbons, has largely corrected the trouble. Calculate the volume occupied past x.0 thou of each of these compounds at STP:
    1. CCl₂F₂(g)
    2. CH₃CH₂F(1000)
27. As 1 g of the radioactive element radium decays over i year, it produces one.16 × ten¹⁸ alpha particles (helium nuclei). Each alpha particle becomes an atom of helium gas. What is the pressure in pascal of the helium gas produced if it occupies a volume of 125 mL at a temperature of 25 °C?
28. A balloon that is 100.21 L at 21 °C and 0.981 atm is released and just barely clears the top of Mount Crumpet in British Columbia. If the last volume of the balloon is 144.53 L at a temperature of v.24 °C, what is the pressure level experienced past the balloon as information technology clears Mountain Crumpet?
29. If the temperature of a fixed amount of a gas is doubled at constant volume, what happens to the pressure level?
30. If the volume of a fixed amount of a gas is tripled at abiding temperature, what happens to the pressure level?

Glossary

absolute zero:temperature at which the volume of a gas would be zero according to Charles's constabulary.

Amontons's police force:(besides, Gay-Lussac'southward law) pressure of a given number of moles of gas is straight proportional to its kelvin temperature when the volume is held constant

Avogadro'south police:volume of a gas at constant temperature and pressure is proportional to the number of gas molecules

Boyle's police:volume of a given number of moles of gas held at constant temperature is inversely proportional to the pressure under which it is measured

Charles'south law:volume of a given number of moles of gas is directly proportional to its kelvin temperature when the pressure is held constant

ideal gas:hypothetical gas whose physical properties are perfectly described by the gas laws

ideal gas constant (R):constant derived from the platonic gas equation R = 0.08226 Fifty atm mol^–1 1000^–1 or viii.314 L kPa mol^–1 1000^–i

ideal gas police:relation between the pressure, volume, corporeality, and temperature of a gas under atmospheric condition derived past combination of the simple gas laws

standard atmospheric condition of temperature and pressure (STP):273.15 Yard (0 °C) and 1 atm (101.325 kPa)

standard molar book:volume of one mole of gas at STP, approximately 22.iv L for gases behaving ideally

dicktrupoo.blogspot.com

Source: https://courses.lumenlearning.com/suny-mcc-chemistryformajors-1/chapter/relating-pressure-volume-amount-and-temperature-the-ideal-gas-law/

Share this post